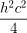Tópico 06: Área de Polígonos com n lados
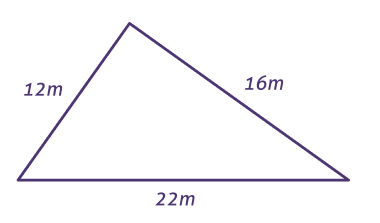
Vamos obter no próximo exemplo a fórmula da área do polígono regular de n lados, lembrando que num polígono regular os comprimentos dos lados assim como os ângulos internos formados por lados adjacentes são iguais entre si.
É comum chamar a metade do perímetro de semiperímetro. Dessa forma, podemos também dizer que a área de um polígono regular é igual ao produto do apótema pelo semiperímetro.
Polígonos quaisquer
Não existe fórmula fechada para a área de um polígono arbitrário, mas existe um método que pode ser empregado quando é possível calcular as distâncias entre quaisquer dois vértices da figura: todo polígono pode ser repartido em triângulos disjuntos, trançando alguns dos segmentos que ligam vértices do polígono (chamamos isso de “triangularizar o polígono”). Daí, podemos calcular a área do polígono somando as áreas desses triângulos (que, por sua vez, podem ser calculadas de diferentes maneiras, a depender de quais informações temos disponíveis).
Esse método é ilustrado na Figura seguinte:
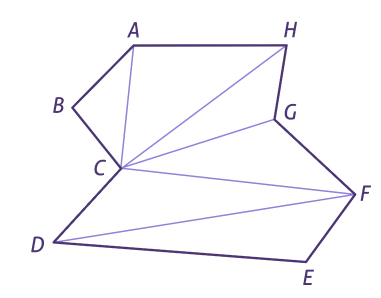
O polígono ABCDEFGH é a união dos triângulos ABC, ACH, CGH, CFG, CDF e DEF e a área do polígono é a soma das áreas desses triângulos. A triangularização de um polígono não é única. Por exemplo, poderíamos substituir o segmento DF por CE e obter outra triangularização.
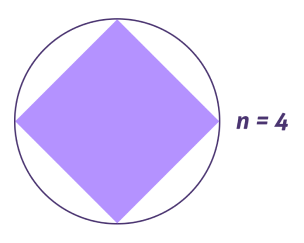
Na antiguidade, os agrimensores provavelmente utilizavam o método da triangularização do polígono para determinar a área das propriedades rurais. Inicialmente aproximavam os terrenos por polígonos irregulares, que decom- punham em triângulos (eles conheciam técnicas para medir os lados desses triângulos). Calculavam as suas áreas, possivelmente pela chamada fórmula de Herão, conhecida já na antiguidade. Essa fórmula fornece uma maneira alternativa de calcular áreas de triângulos tendo conhecimento apenas das medidas de seus três lados, evitando a necessidade de calcular a medida de uma altura. Se os lados possuem medidas a, b e c, primeiro calcula-se o se- miperímetro, que é p = (a + b + c)/2 e, então, a área do triângulo é dada por:
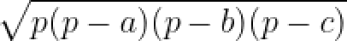
A área do terreno, então, é a soma das áreas desses triângulos.
Embora a dedução da fórmula de Herão não faça parte do conteúdo didático do ensino médio, apresentamos uma seção com a dedução algébrica da fórmula de Herão para aqueles alunos que tenham curiosidade de conhecer sua origem.
Você consegue imaginar por que os gregos antigos chamavam os geômetras egípcios do seu tempo de “esticadores de corda”? Pense em como os egípcios delimitavam os terrenos e os dividiam em triângulos com os recursos limitados que dispunham na época.
No mundo moderno, é possível aproximar a área de um terreno usando um GPS para marcar as coordenadas cartesianas dos vértices de um polígono que delimita (ainda que de forma aproximada) o contorno do terreno. De posse dessas coordenadas é possível calcular as distâncias entre os pontos (pelo teorema de Pitágoras, como explicado no Módulo 11) e de posse dos comprimentos dos lados dos triângulos é possível aplicar a fórmula de Herão para obter suas áreas. Mas, de posse das coordenadas dos vértices, há outras maneiras ainda mais eficientes de calcular a área do polígono que fogem do escopo deste módulo (por exemplo, usando matrizes). Em geral, esses cálculos são efetuados por aplicativos cujo funcionamento interno é ignorado pelo usuário final.
Fórmula de Herão

Dedução da Fórmula de Herão
O desafio é apresentar uma prova para a fórmula de Herão mostrando que ela realmente calcula a área do triângulo. Apresentaremos uma prova algébrica com muitos cálculos que deixamos aqui para satisfazer a curiosidade dos alunos que se perguntarem por que a fórmula funciona.
Como conhecemos a fórmula da área do triângulo como , o desafio é calcular a altura h em função dos lados do triângulo.
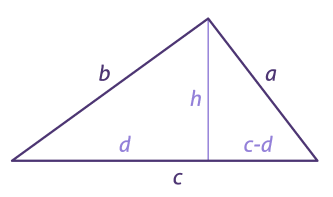
Ao traçarmos a altura em relação à base c, obtemos dois triângulos retângulos de onde tiramos:
b2 = h2 + d2
a2 = h2 + (c – d)2
Daí,
a2 – b2 = (c – d)2 – d2
a2 – b2 = c2 – 2cd
Daí,
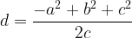
Na dedução da fórmula, partimos do fato de que h2= b2 – d2 e usamos repetidamente o produto notável a2 – b2 = (a + b)(a – b).
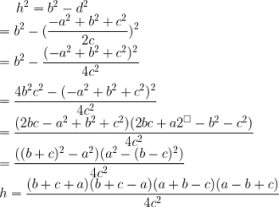
Lembre-se que p=
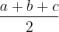
a +b +c = 2p
b + c – a = 2p – 2a = 2(p – a).
a + b – c = 2p – 2c = 2(p – c).
a – b + c = 2p – 2b = 2(p – b).
Continuando,
Área do triângulo, A =
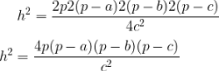
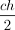
Assim,